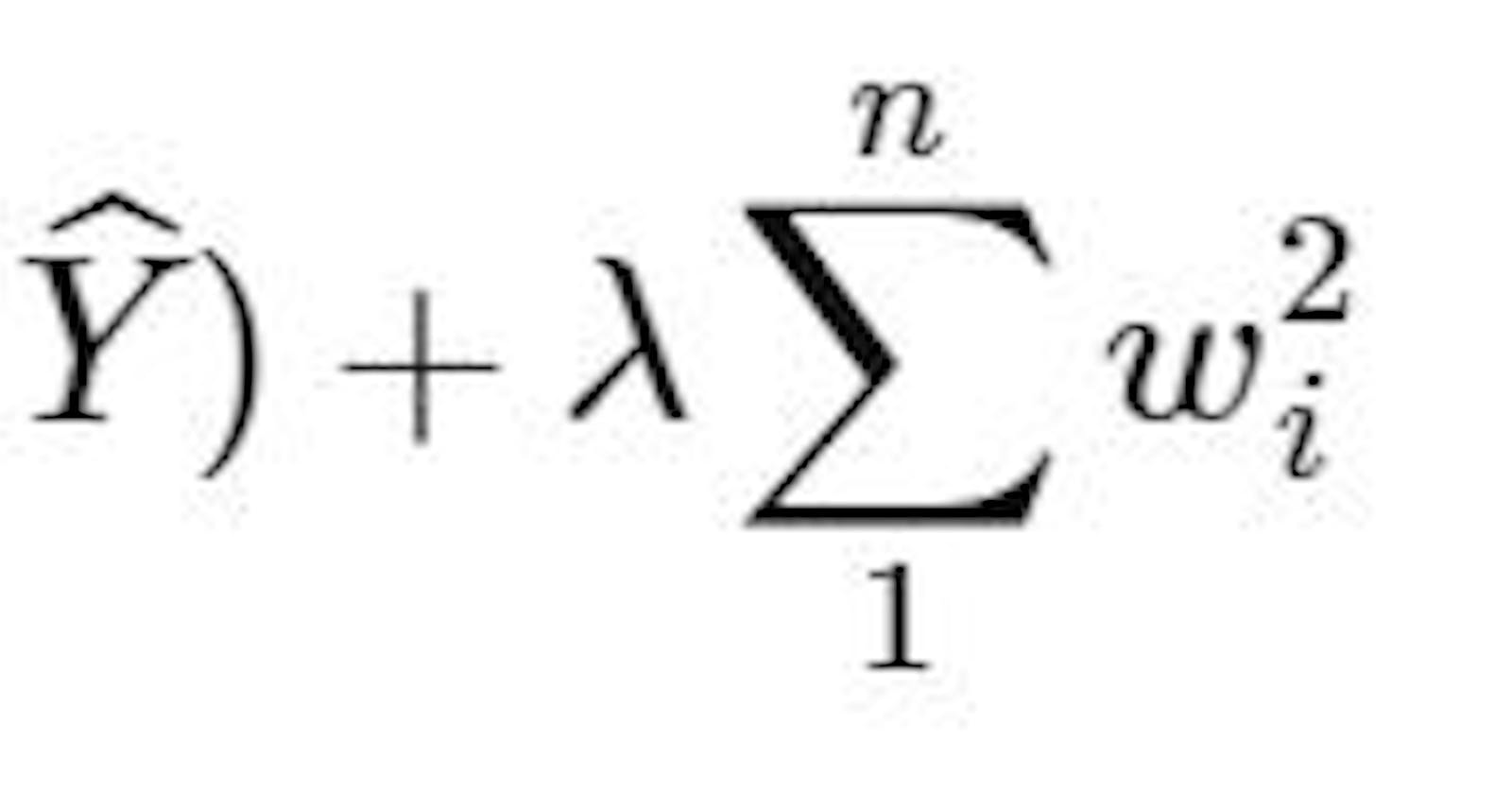Regularization is a technique used in machine learning to prevent overfitting and reduce variance in a model. Overfitting occurs when a model is excessively complex and has learned even the noise in the training data, which can negatively impact the model's ability to generalize to new data.

There are several types of regularization techniques, each of which adds a penalty to the loss function during training to encourage the model to learn a simpler and more generalized decision boundary. They are as follows:

L1 Regularization:

L1 regularization, also known as Lasso regularization, adds a penalty term to the loss function equal to the absolute value of the weights multiplied by a hyperparameter alpha or lambda. This results in sparse models, where some weights are exactly equal to zero, effectively removing those features from the model.

Here is the mathematical representation:

$$Loss = Error(Y - \widehat{Y}) + \lambda \sum_1^n |w_i|$$

Here is an example of L1 regularization in TensorFlow:

import tensorflow as tf

# create a model with L1 regularization
model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, input_shape=(8,), kernel_regularizer=tf.keras.regularizers.l1(0.01))
])

# compile the model with a loss function and an optimizer
model.compile(loss='mean_squared_error', optimizer='sgd')

Here, the regularization term is set to 0.01. If you keep increasing this value, the model gets simpler and simpler.

L2 Regularization:

L2 regularization, also known as Ridge regularization, adds a penalty term to the loss function equal to the square of the weights multiplied by a hyperparameter alpha or lambda. This results in a smooth model, where the magnitude of the weights is small but not necessarily equal to zero. The 2 in L2 represents the squaring of the weights.

Here is the mathematical representation of L2:

$$Loss = Error(Y - \widehat{Y}) + \lambda \sum_1^n w_i^{2}$$

Here is an example of L2 regularization in TensorFlow:

import tensorflow as tf

# create a model with L2 regularization
model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, input_shape=(8,), kernel_regularizer=tf.keras.regularizers.l2(0.01))
])

# compile the model with a loss function and an optimizer
model.compile(loss='mean_squared_error', optimizer='sgd')

Elastic Net Regularization:

Elastic Net regularization is a combination of L1 and L2 regularization, where the penalty term is a combination of both absolute and square values of the weights multiplied by hyperparameters alpha and l1_ratio.

Here is an example of Elastic Net regularization in TensorFlow:

import tensorflow as tf

# create a model with Elastic Net regularization
model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, input_shape=(8,), kernel_regularizer=tf.keras.regularizers.l1_l2(0.01, 0.5))
])

# compile the model with a loss function and an optimizer
model.compile(loss='mean_squared_error', optimizer='sgd')

Dropout Regularization:

Dropout regularization is a technique used very often in neural networks, where a random fraction of the neurons is "dropped out" or turned off during training. This has the effect of reducing overfitting and improving the generalization of the model. The idea behind this is that at every iteration, the size of the neural network is reduced by a certain percentage. This percentage is called the Dropout Rate

Here is an example of Dropout regularization in TensorFlow:

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(8,), activation='relu'),
    tf.keras.layers.Dropout(0.5),
    tf.keras.layers.Dense(1, activation='sigmoid')
])